ELU for RNN

ML Low hanging Fruit: If you are using RNN for long dependencies: Try ELU

Recurrent Neural Networks (RNN) have difficulty to learn long depencies due to vanishing and exploding gradients. Quoc et al (paper) suggested to use identity matrix for hidden to hidden matrix initialization for using ReLU units in RNN (=Identity RNN or IRNN).

Experiments suggest that recently introduced ELU (Exponential Linear Unit) can outperform ReLU and converge quite faster than ReLU.

The graph below shows accuracy vs epochs for Sequential MNIST Task i.e feeding one pixel at a time (784 time steps in RNN terminology for 28*28 image).

ELU reaches 96+ accuracy easily vs ReLU struggling to come close.

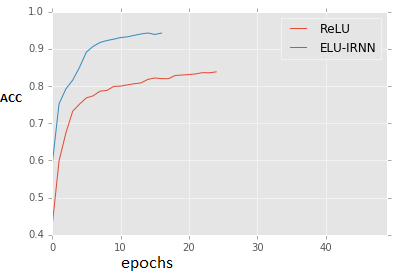
The best accuracy I could get was 97.3 but couldn’t reproduce it. Growth of ELU accuracy may vary (reaching 96+) but within 50 epochs you should see it close by without much learning rate schedule (lower rates when acc. doesn’t change much).

Code for ELU can be easily experimented with beautiful lib keras:

keras MNIST IRNN code Just use :

import theano.tensor as T
def elu(x,alpha=1.0):

        return T.nnet.elu(x, alpha)
        
SimpleRNN(output_dim=hidden_units,

                    init=lambda shape, name: keras.initializations.glorot_normal(shape, name=name),
                    inner_init=lambda shape,name :keras.initializations.identity(shape,name),
                    activation = elu,                    
                    input_shape=X_train.shape[1:])

Anybody with PTB (Penn Tree Bank Corpus) acces can replicate PTB experiment to confirm my findings and check against this : path Normalized SGD with IRNN paper. I want to see if we reach nearby LSTM with ELU. Please comment or email.